100 Nickels Is How Much

Learning Outcomes

Determine the value of a given number of coins
Apply the problem-solving method to solve discussion issues involving coins

Imagine taking a scattering of coins from your pocket or purse and placing them on your desk. How would you decide the value of that pile of coins?

If you can grade a step-by-step plan for finding the full value of the coins, it will aid you equally you begin solving coin word problems.

I way to bring some order to the mess of coins would be to separate the coins into stacks co-ordinate to their value. Quarters would go with quarters, dimes with dimes, nickels with nickels, and so on. To go the total value of all the coins, you lot would add the total value of each pile.

A small stack of dimes, a slightly larger stack of nickels, and a slightly larger stack of quarters, all lined up on a glossy table with their reflections showing To make up one's mind the full value of a stack of nickels, multiply the number of nickels times the value of 1 nickel.

How would you lot determine the value of each pile? Think about the dime pile—how much is information technology worth? If you count the number of dimes, yous'll know how many you accept—the number of dimes.

Only this does not tell y'all the value of all the dimes. Say you lot counted

$17$

dimes; how much are they worth? Each dime is worth

$\text{\$0.x}$

—that is the value of 1 dime. To discover the total value of the pile of

$17$

dimes, multiply

$17$

past

$\text{\$0.ten}$

to become

$\text{\$ane.70}$

. This is the full value of all

$17$

dimes.

$\begin{array}{c}\qquad 17\cdot \text{\$0.10}=\text{\$1.70}\qquad \\ \qquad \text{number}\cdot \text{value}=\text{full value}\qquad \finish{array}$

Finding the Full Value for Coins of the Same Type

For coins of the same type, the full value can be constitute every bit follows:

$\text{number}\cdot \text{value}=\text{total value}$

where number is the number of coins, value is the value of each coin, and total value is the total value of all the coins.

You could continue this process for each type of coin, and then yous would know the total value of each type of coin. To get the full value of all the coins, add the full value of each blazon of coin.

Let's look at a specific example. Suppose there are

$14$

quarters,

$17$

dimes,

$21$

nickels, and

$39$

pennies. We'll brand a table to organize the information – the type of coin, the number of each, and the value.

Type	$\text{Number}$	$\text{Value (\$)}$	$\text{Full Value (\$)}$
Quarters	$14$	$0.25$	$3.fifty$
Dimes	$17$	$0.ten$	$1.seventy$
Nickels	$21$	$0.05$	$one.05$
Pennies	$39$	$0.01$	$0.39$
			$half-dozen.64$

The total value of all the coins is

$\text{\$6.64}$

. Notice how the higher up table helped the states organize all the information.

Allow's review the trouble-solving method for give-and-take bug.

PROBLEM-SOLVING STRATEGY

Step 1. Read the problem. Make sure y'all understand all the words and ideas.

Stride 2. Place what you are looking for.

Pace three. Name what you are looking for.

Step iv. Translate into an equation. Restate the problem in one sentence. Then translate into an equation.

Step 5. Solve the equation using adept algebra techniques.

Step 6. Check.

Stride seven. Answer the question.

Let'southward see how this method is used to solve a coin give-and-take problem.

Example

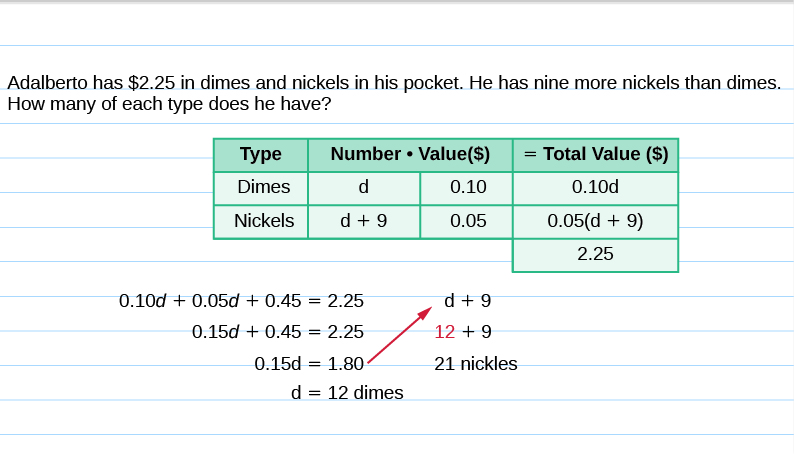
Adalberto has

$\text{\$2.25}$

in dimes and nickels in his pocket. He has nine more than nickels than dimes. How many of each blazon of money does he take?

Solution:

Step 1. Read the problem. Make sure yous understand all the words and ideas.

Make up one's mind the types of coins involved.

Retrieve virtually the strategy nosotros used to observe the value of the scattering of coins. The first matter you need is to notice what types of coins are involved. Adalberto has dimes and nickels.

Create a table to organize the information.
- Label the columns "blazon", "number", "value", "full value".
- List the types of coins.
- Write in the value of each type of money.
- Write in the total value of all the coins.

We can work this problem all in cents or in dollars. Hither nosotros will do information technology in dollars and put in the dollar sign ($) in the table as a reminder.

The value of a dime is

$\text{\$0.10}$

and the value of a nickel is

$\text{\$0.05}$

. The total value of all the coins is

$\text{\$2.25}$

Type	$\text{Value (\$)}$	$\text{Total Value (\$)}$
Dimes	$0.ten$
Nickels	$0.05$
		$2.25$

Step two. Identify what you are looking for.

We are asked to find the number of dimes and nickels Adalberto has.

Step 3. Name what yous are looking for.

Use variable expressions to stand for the number of each type of money.
Multiply the number times the value to get the total value of each type of coin. In this problem you cannot count each blazon of coin—that is what you are looking for—but y'all have a clue. There are nine more nickels than dimes. The number of nickels is nine more the number of dimes.
$\text{Let }d=\text{number of dimes.}$

$\text{Let }d+9=\text{number of nickels.}$
Fill up in the "number" cavalcade to help go everything organized.

Type	$\text{Number}$	$\text{Value (\$)}$	$\text{Total Value (\$)}$
Dimes	$d$	$0.10$
Nickels	$d+9$	$0.05$
			$ii.25$

Now we have all the information we need from the problem!

You multiply the number times the value to go the total value of each type of coin. While you do non know the bodily number, yous practise accept an expression to correspond information technology.

And then at present multiply

${\text{number}}\cdot {\text{value}}$

and write the results in the Total Value column.

Type	$\text{Number}$	$\text{Value (\$)}$	$\text{Total Value (\$)}$
Dimes	$d$	$0.ten$	$0.10d$
Nickels	$d+9$	$0.05$	$0.05\left(d+9\right)$
			$2.25$

Step 4. Translate into an equation. Restate the problem in 1 sentence. So translate into an equation.

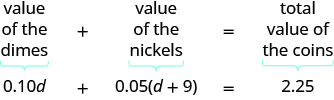The sentence Footstep v. Solve the equation using good algebra techniques.

Write the equation.	$0.10d+0.05(d+9)=ii.25$
Distribute.	$0.10d+0.05d+0.45=ii.25$
Combine like terms.	$0.15d+0.45=2.25$
Decrease 0.45 from each side.	$0.15d=one.80$
Divide to observe the number of dimes.	$d=12$
The number of nickels is d + 9	$d+nine$ $\colour{ruby-red}{12}+nine$ $21$

Pace vi. Bank check.

$\begin{array}{ccc}12 dimes: 12\left(0.10\correct)\qquad & =\qquad & 1.twenty\qquad \\ 21\text{ nickels: }21\left(0.05\right)\qquad & =\qquad & \underset{\text{------}}{1.05}\qquad \\ & & \text{\$2.25}\quad\checkmark \qquad \end{array}$

Stride vii. Answer the question.

$\mathit{\text{Adalberto has twelve dimes and twenty-one nickels.}}$

If this were a homework exercise, our piece of work might look like this:

How many of each type does he have?

Solve a coin word trouble

Read the problem. Brand certain you understand all the words and ideas, and create a table to organize the information.
Identify what you lot are looking for.
Proper noun what you are looking for. Choose a variable to correspond that quantity.
- Use variable expressions to stand for the number of each type of coin and write them in the table.
- Multiply the number times the value to get the total value of each type of coin.
Translate into an equation. Write the equation by adding the total values of all the types of coins.
Solve the equation using skilful algebra techniques.
Cheque the respond in the problem and brand certain it makes sense.
Answer the question with a complete judgement.

Yous may find it helpful to put all the numbers into the table to make sure they check.

Type	Number	Value ($)	Full Value

Case

Maria has

$\text{\$two.43}$

in quarters and pennies in her wallet. She has twice every bit many pennies every bit quarters. How many coins of each type does she have?

Show Solution

In the side by side instance, we'll evidence just the completed tabular array—make certain y'all understand how to fill up it in step by step.

Example

Danny has

$\text{\$2.fourteen}$

worth of pennies and nickels in his piggy bank. The number of nickels is ii more than ten times the number of pennies. How many nickels and how many pennies does Danny have?

Show Solution

In the post-obit video we evidence some other case of how to solve a word problem that involves finding an amount of coins.

Licenses and Attributions